Thanks to incredible leaps in technology over the last few decades, navigation has become incredibly simple. Instead of finding where you are and where you’re going on a map, now we just ask our phones how to get wherever we’re going.
Many navigation applications use an algorithm called the Dijkstra algorithm to find the most efficient route. Dijkstra’s algorithm was conceived by computer scientist Edsger W. Dijkstra in 1956 and is used to find the shortest path between nodes in a graph. This applies perfectly to networks of roads. This algorithm has become the backbone of nearly all navigation applications in recent years. It really enables so much of our lives and yet goes by completely unnoticed by the majority of people.
I’ll be using Google Maps as an example throughout this as it’s something that most people have had experience and are familiar with. Applications like Google Maps look at the streets as a graph which consists of nodes. These nodes are locations on the map, with edges (roads) connecting different these nodes.
When you try to navigate from one node to another (one location to another), the route is composed of different edges (roads) you can travel on. To better explain, here’s a map with a representation of nodes drawn over it.

Let’s say you want to go from node 25 (top left corner), to node 23 (middle-left). There are many different routes joining these nodes, and every such route is defined by a series of edges we take from node to node:
• 25–24–23
• 25–27–23
• 25–24–19–18–10–11–17–20–23
The question is now a bit more simple: how do we find all the possible routes, and which route is the most efficient?
Finding Routes:
To find all the possible routes, the Dijkstra algorithm uses a relatively straightforward process:
• Look at the starting position/node – in our case we’re starting at node 25.
• Consider all the nodes connected to this node by an edge – nodes 24 and 27.
• If one of these is the target node (our destination) – stop. We have an edge that gets us there.
• If none of these are the target edge, repeat the process for each one of the nodes found, using it as a starting node. We already have a path to get to them, so if there’s a path to get from them to the target, we can join the two.
Route Value:
We can give each edge (line connecting 2 nodes) a value. This value will represent the time taken to travel that edge or the time it takes us to travel along that road.
Depending on the application, this cost will be impacted by many parameters, including:
• Length of the road
• Number of lanes
• Traffic lights
• Traffic data (real time / estimate)
• Toll roads, motorways, etc
In the map shown above there is a blue number above every edge – this is the value. Our goal is to find the route with the lowest value, which will be translated to the shortest time or most efficient way of travelling somewhere.
The algorithm can be adjusted slightly to do this:
Put the start node into a priority queue (which will return the lowest value), with a value of 0.
We then repeat the following:
• Pull the node A with lowest cost from queue
• If this is the target node, we have a route!
• If this isn’t the target node, we pull all of the nodes connected to it with an edge.
• For each of these neighbouring nodes B, we put them back into the queue, with the combined cost of getting to A (from the queue) plus the cost of getting from A-B.
Another visual representation of this may help to grasp the concept easier.
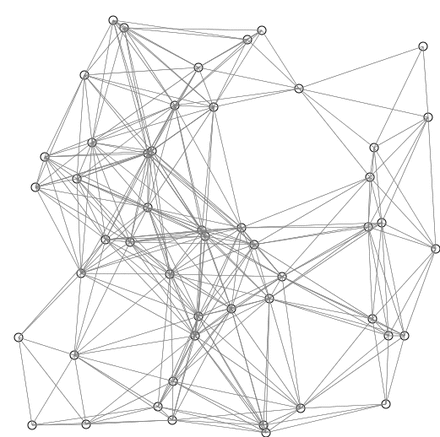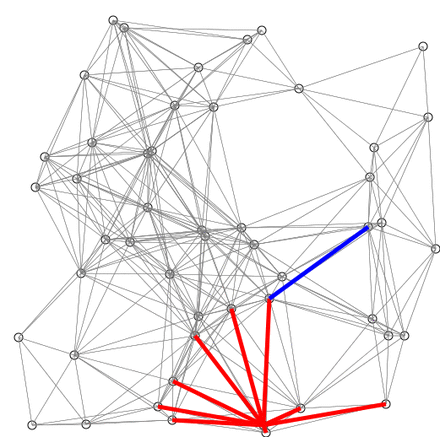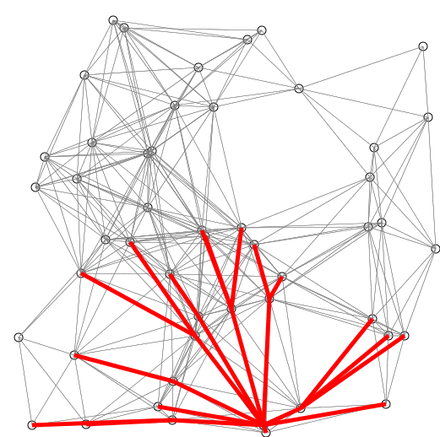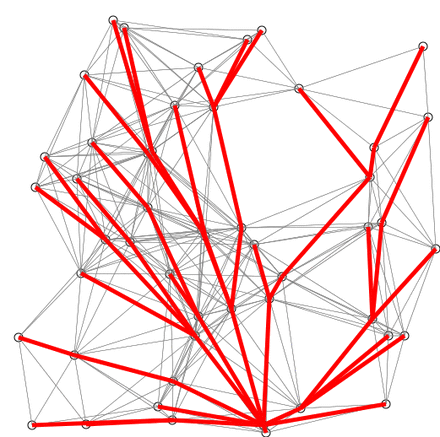
This is an example of Dijkstra’s algorithm based on Euclidean distance. Red lines are the shortest path connecting two nodes. Blue lines indicate where relaxing happens.